对三组数据基尼系数的估算
【内容提要】本文介绍一个粗略估算基尼系数的方法,并根据三组公开的经济数据,对其基尼系数进行了估算。
1.从三张截图谈起
先看下面 三张截图:

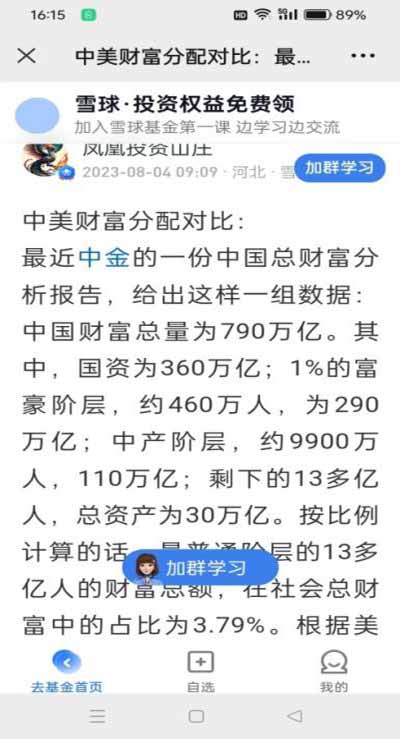
第一张,是来自于国家统计局2024年2月29日发布的2023年经济数据。这里把全国居民人均年收入按居民5等份分组。
第二张,是中金公司给出的中国总财富分布数据(分4组)。
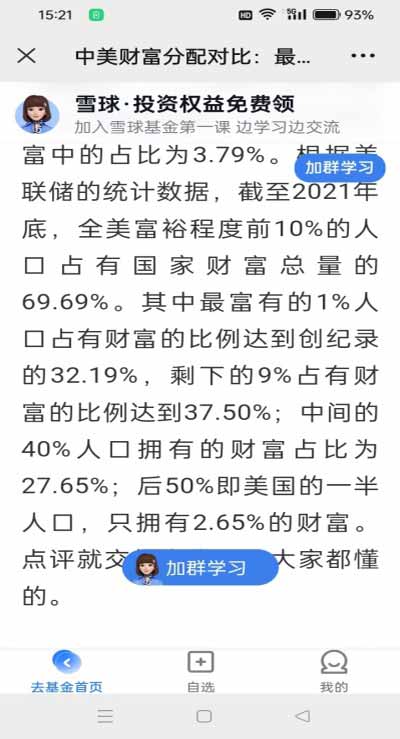
第三张,是美联储统计的全美总财富的分布数据(分4组)。
面对截图中的数据,作为外行的我们,能不能设法估量一下国民收入(或财富)贫富差距的大小呢?这就不能不谈到基尼系数和洛伦兹曲线。
2.关于洛伦兹曲线
大家知道,基尼系数G是用来衡量某国或某地贫富差距的一个比值。一般认为:G<0.2时居民收入过于平均;0.2-0.3之间时较为平均;0.3-0.4时比较合理;0.4-0.5时差距过大;G>0.5时差距悬殊。
其正规的计算方法是通过洛伦兹(M·O·Lorenz)曲线来进行的(如图):
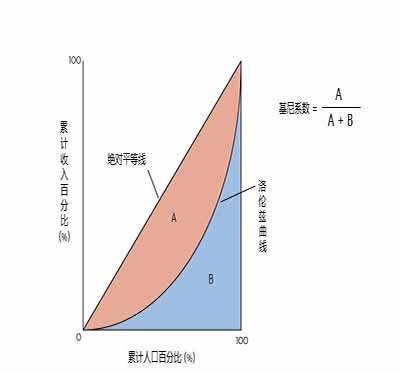
要得到这条曲线:(1)首先要通过大量的调查研究,去得知某地全体(或样本)每一个人的收入数;(2)计算出每个人的收入在总收入中所占的百分比;(3)把这些百分比由低到高排成一行数据;(4)计算这些百分比数据累计之和y ;(5)计算累计人数百分比x ;(6)建立直角坐标系XOY,将这些点(x,y) 一个一个标在坐标系上;(7)积点成线 ,得到图中的洛伦兹曲线。
然后才能求图中B、(A+B)、A的面积,计算基尼系数G。如此海量的调查 、统计、计算、绘图工作,不是专业人士操作电脑,是 很难完成的。
那么,对于非专业的普通大众,面对别人调查研究后给出的有限数据,有没有简单的、粗略的、估算基尼系数的方法呢?这里介绍一个主要用加减乘除的估算方法——“折线法”(当然还有一点技巧)。
3.举个简单例子
【引例】假定有100个人平均分成5组,各组人均月收入分别是1、2、3、4、5(千元)。试求其月收入的基尼系数。
万事起头难,下面的计算比较琐细,要耐下心来看。对算法不感兴趣的读者不妨跳过这两节,直接看最后一节“算法应用举例”。
(1)首先算人数百分比:各小组都占20%,那么累计百分比依次就是20%、40%、60%、80%、100%。
(2)再算收入百分比。各组收入合计数分别为2万元、4万元、 6万元、8万元、10万元,总计30万元。各组占比分别为:2÷30=6.67%,4÷30=13.33%,20%,26.67%,33.33%。累计收入百分比 依次为:6.67%, 20%,40%,66.67%,100%。
(3)因此,尚未画出的坐标系中关键点的坐标(化成小数后)分别是A(0.2,0.0667)、B(0.4,0.2)、C(0.6,0.4)、D(0.8,0.6667)、E(1,1)。
充分准备后,方可画出直角坐标系(如图):
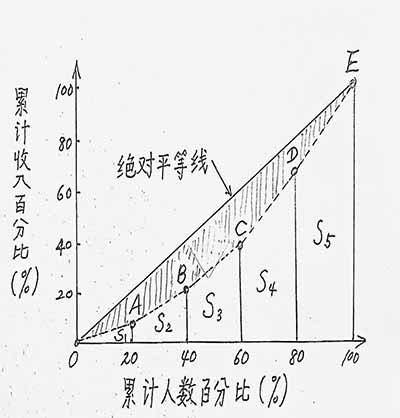
由于数据太少,得不出洛伦兹曲线,只能画出一条折线(这意味着假定各小组内部成员收入绝对平均)来逼近它。图中一个三角形和四个梯形的面积之和相当于彩图中的B的面积。
计算S1=0.0667×0.2÷2=0.0067;
S2=(0.0667+0.2)×0.2÷2=0.0267;
S3=(0.2+0.4)×0.2÷2=0.06 ;
S4=0.1067 ; S5=0.1667 ;
SB=S1+S2+S3+S4+S5=0.3667 。
而 SA+B= 1×1÷2=0.5,
所以 SA=0.5-0.3667=0.1333。
G=SA÷SA+B= 0.1333÷0.5=0.2667。
以上,通过不厌其烦的百分比运算,得出这100个人月收入的基尼系数为0.2667。但这只是用“折线法”计算出来的近似值,它小于真正的基尼系数G(估计能小5%-10%)。
事实上,如果不把人数和月收入数都计算出百分比,而是适当改变一下原始数据,并不会影响计算的结果。比如我们把横坐标扩大5倍,纵坐标扩大15倍,则得到一个新坐标系(图略)。那么图中6个点的新坐标将分别是:O(0,0)、A(1,1)、B(2,3)、C(3,6)、D(4,10)、E(5,15)。在新坐标系中 :
S1=(0+1)×(1-0)÷2=0.5 ; S2=(1+3)×(2-1)÷2=2;
S3=4.5 ;S4=8,S5=12.5,SB=27.5 ; SA+B=(15×5)÷2=37.5。
所以,基尼系数G = SA÷SA+B=(37.5-27.5)÷37.5=0.2667。这样计算就简单多了。
4.总结估算方法
从上面例子可以看出,本文介绍的估算方法不仅在于用“折线法”求梯形类面积之和去逼近SB(这是大家都采用的方法),还在于:在两坐标轴上(人数和收入)的标注方法不拘泥于百分比:(1)既可以用百分比;(2)也可以用原始数据;(3)又可以适当扩大或缩小原数据。这并不会影响计算结果的正确性。用哪种数据计算,仅仅为了方便。
下面把算法步骤总结一下 :
1.题目中一般都按人们收入由少到多把总人数分成了n个小组,并给出了各小组人数以及各小组人均收入数。第一步先要考虑是否改变人数和收入数的原数据(上面三法选一),并确定下来,用新数据进行计算;
2.计算出前若干个小组人数累计数x;
3.计算各小组的总收入数;
4.计算前若干个小组总收入累计数y;
5.写出未来图中各点的坐标:A(x1,y1),B(x2,y2),C(x3,y3),……;
6.画出直角坐标系XOY,标注坐标轴上的刻度,在图中标出关键点A、B、C……,画出折线及各个梯形等等;
7.计算各梯形类图形面积S1、S2、…,Sn;
8.计算SB、SA+B、SA和基尼系数G(算法见前面例子)。
5.算法应用举例
【例1】2024年2月29日,国家统计局发布了许多经济数据。截图1是其中的我国2023年“按居民五等分年收入分组”。抄写数据如下:
低收入20%人口 9215元;中下收入20%人口20442元;
中等收入20%人口32195元; 中上收入20%人口 50220元;
高收入20%人口95055元。
但国家统计局并没有公布2023年居民收入的基尼系数G。(自2016年后再没公布过。 据说是因为无法得知某些高收入人士的真实收入,所以计算的基尼系数偏离实际,不宜公布。)
下面,我们试用这些数据估算一下2023年我国居民年收入的基尼系数,看看这个G大概是多少?
(1)首先,这里给出的原始人口数据的各组百分比都是0.2,我们可以把0.2作为标注X轴的刻度,但我们也不妨扩大5倍,令它们都变成1,计算会更简单(纵坐标Y就用原始数据)。
(2)列表计算(设我国总人口为14亿)
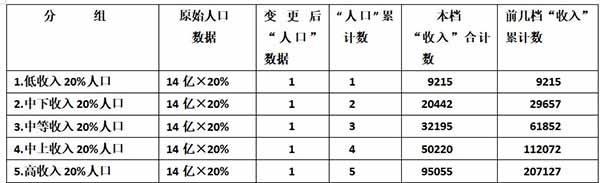
(3)写出未来坐标系中各点坐标:
A(1,9215) B(2,29657) C(3,61852)
D(4,112072) E(5,207127)
(4)画出直角坐标系以及各图形:
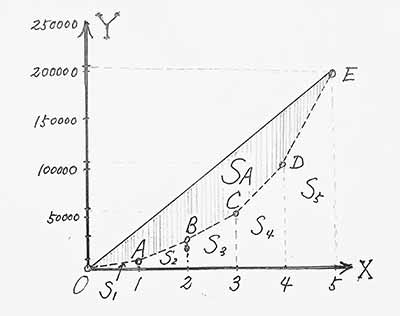
(5)根据图形计算SB、SA+B、SA以及基尼系数G:
S1=9215×1÷2=4607.5 ,
S2=(9215+29657)×(2-1)÷2=19436,
S3=45754.5,S4=86962,S5=159599.5.
求和得SB=316359.5, 然后求得SA+B=517817.5, SA=201458 。
所以,估算的基尼系数G=SA÷SA+B=0.38905(明显偏小!)
【例2】根据截图2里中金公司报告的数据(不再重抄了),估算中国民间总财富430万亿划分的基尼系数(国资类360万亿已除外)。
然而,什么是“财富”呢?是使用价值还是交换价值?只是现金、存款和证券?或是包括房地产在内的资产?还是泛指“所有值钱的东西”(包括服务、知识、健康、青春、关系等等)?这些,在经济学上并无定论。这里的财富大概是指物质方面。但有一点是肯定的:财富不是指年收入,而是指多年(收入减支出后)结余的存量,还有可能是负值。现在不是有个时髦的词叫“负产阶级”吗?
抛开这一切,我们只估算基尼系数G。
先列表并作图(用百分比):
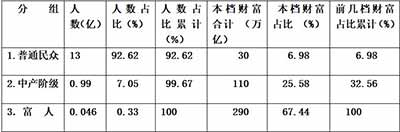
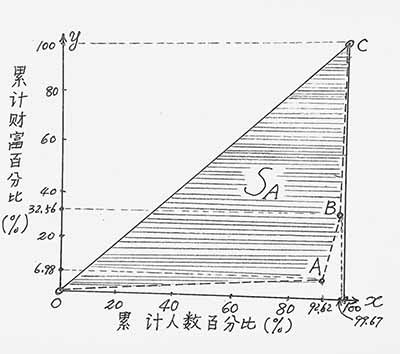
计算面积S1=0.0698×0.9262÷2=0.03232
S2=(0.0698+0.3256)×0.0705 ÷2=0.01394
S3=(0.3256+1)×0.0033÷2=0.002187
所以SB=0.03232+0.01394+0.002187=0.048447
SA=0.5-0.048447 =0.45155
基尼系数 G=0.45155÷0.5=0.9031.
可见财富集聚比起收入分配来,基尼系数要高得多!
【例3】截图3是美联储的统计数据(不再重新抄写),试据此估算截止2021年底全美总财富划分的基尼系数。
由于大家对计算方法已经比较熟悉,这里只列表不画图。
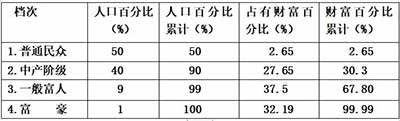
计算如下:
S1=2.65%×50%÷2=0.006625;
S2=(2.65+30.3)%×40%÷2=0.0659;
S3=(30.3+67.8) %×9%÷2=0.04415;
S4=(67.8+99.99)%×1%÷2=0.00839;
SB=0.1251;SA=0.5-0.1251=0.3749;
G=0.3749÷0.5=0.7498。
即:截止2021年底全美总财富划分的基尼系数约为0.7498.
看完例2和例3,不知你有何想法?
最后再重复一遍:用“折线法”估算出来的基尼系数,比真正的
基尼系数G要小一些。 【全文结束】
「 支持!」
您的打赏将用于网站日常运行与维护。
帮助我们办好网站,宣传红色文化!
欢迎扫描下方二维码,订阅网刊微信公众号

